SVM(Support Vector Machine)

KAIST 문일철 교수님의 인공지능 및 기계학습 개론1 수업을 참고하여 정리한 글입니다.
https://www.edwith.org/machinelearning1_17/lecture/10602

1. SVM이란?

데이터를 두 범주로 나누는 문제를 푼다고 생각해 보자.

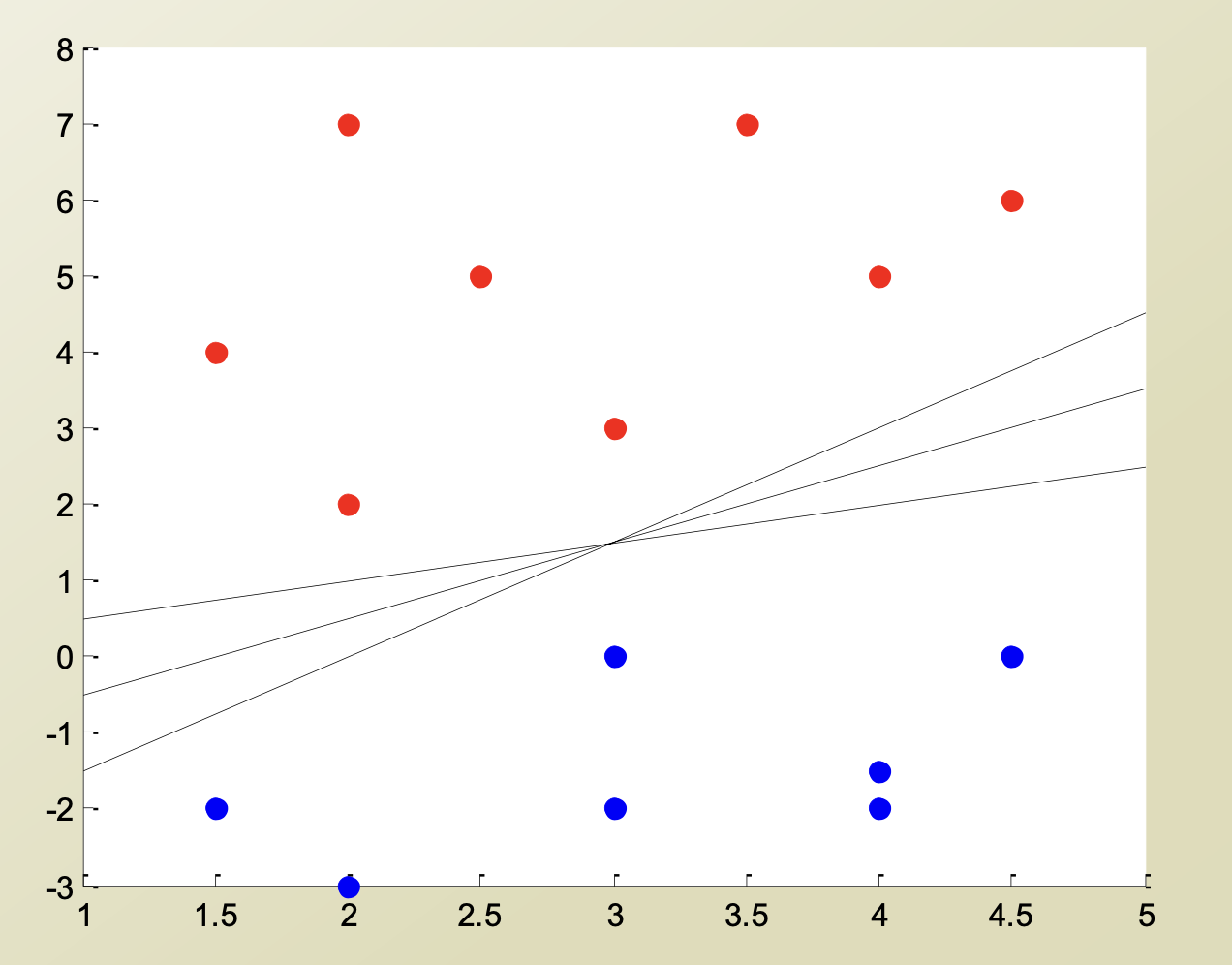
이와 같이 데이터가 존재할 때, 데이터를 두 범주로 나누는 선은 어떻게 정의되어야 할까?
SVM은 이 경계선을 정의하는 모델이다.
여기서 경계선은 Decision Boundary 라고 한다.

2. Decision Boundary

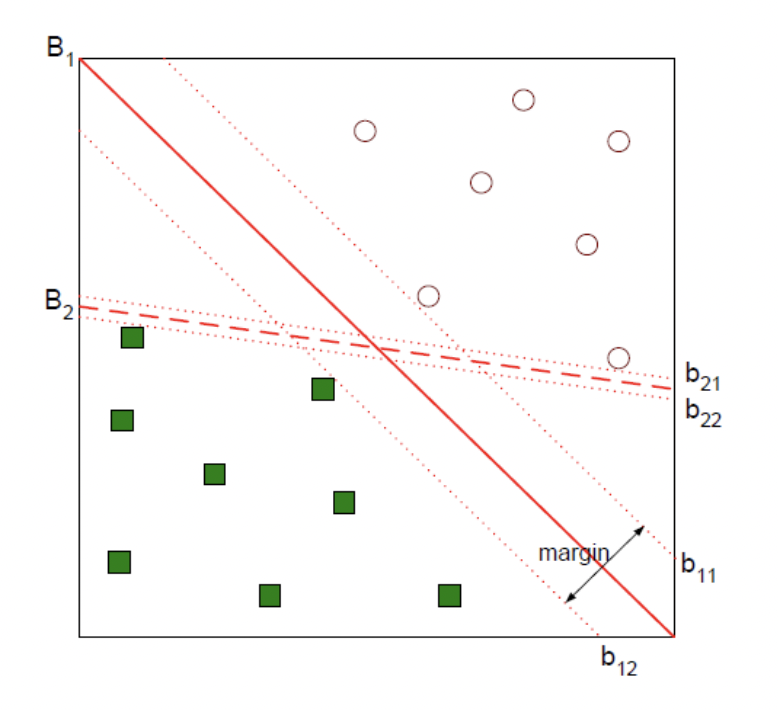
위와 같이 데이터가 분포할 때, 데이터를 두 범주로 나누는 Decision Boundary는 여러가지가 존재한다. 그 중 두가지를 뽑아서 B1, B2로 나타냈는데, 둘 중 어느 것이 Decsion Boundary를 잘 설정했냐고 한다면, B1일 것이다.

그 이유는 그림과 같이 B1에 평행하면서 Decision Boundary 와 가장 근접해 있는 데이터와 맞닿은 선을 b11, b12라고 하고, 두 선 사이의 거리를 margin 이라고 정의했을 때, margin이 커지도록 Decision Boundary를 설정하는 것이 좋기 때문이다.

3. Margin Distance

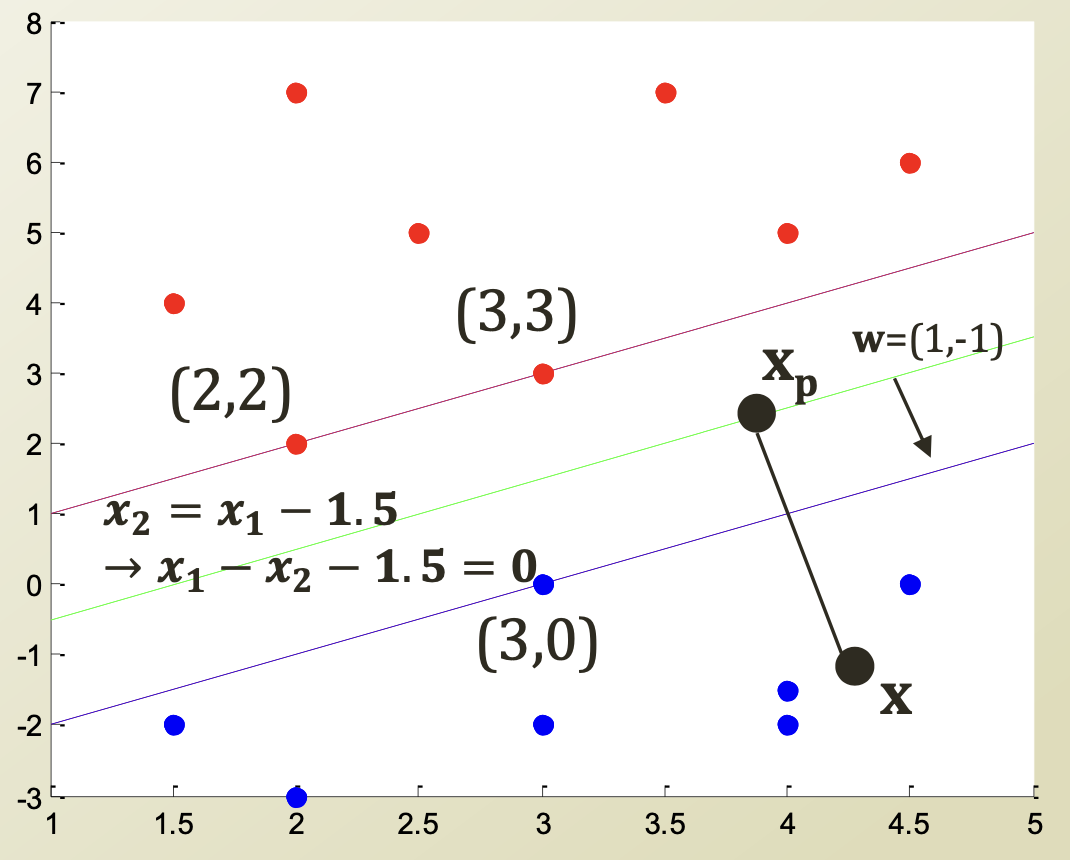
Decision Boundary에 해당하는 직선 함수를 $f(x) = w \cdot x + b$ 라고 할 때,

• A point $x$ on the boundary
  $f(x) = w\cdot x + b = 0$
• A positive point x
  $f(x) = w \cdot x + b = a, a>0$

$x$ 가 $x_p$ 로부터 decision boundary에 수직하게 떨어져 있는 point라 할 때,
$x = x_p + r {w\over { ||w||}}$ 로 나타낼 수 있으며, $f(x_p) = 0$ 이다.
$f(x) = w \cdot x + b = w(x_p + r {w\over||w||}) + b=wx_p + b + r{w\cdot w \over ||w||}= r||w||$ $(\because f(x_p) = w \cdot x_p + b = 0)$
따라서, $x$ 부터 $x_p$까지의 distance인 $r={f(x) \over ||w||}$ 이다.

이제 distance 식을 도출했으니, margin distance를 구해보자.

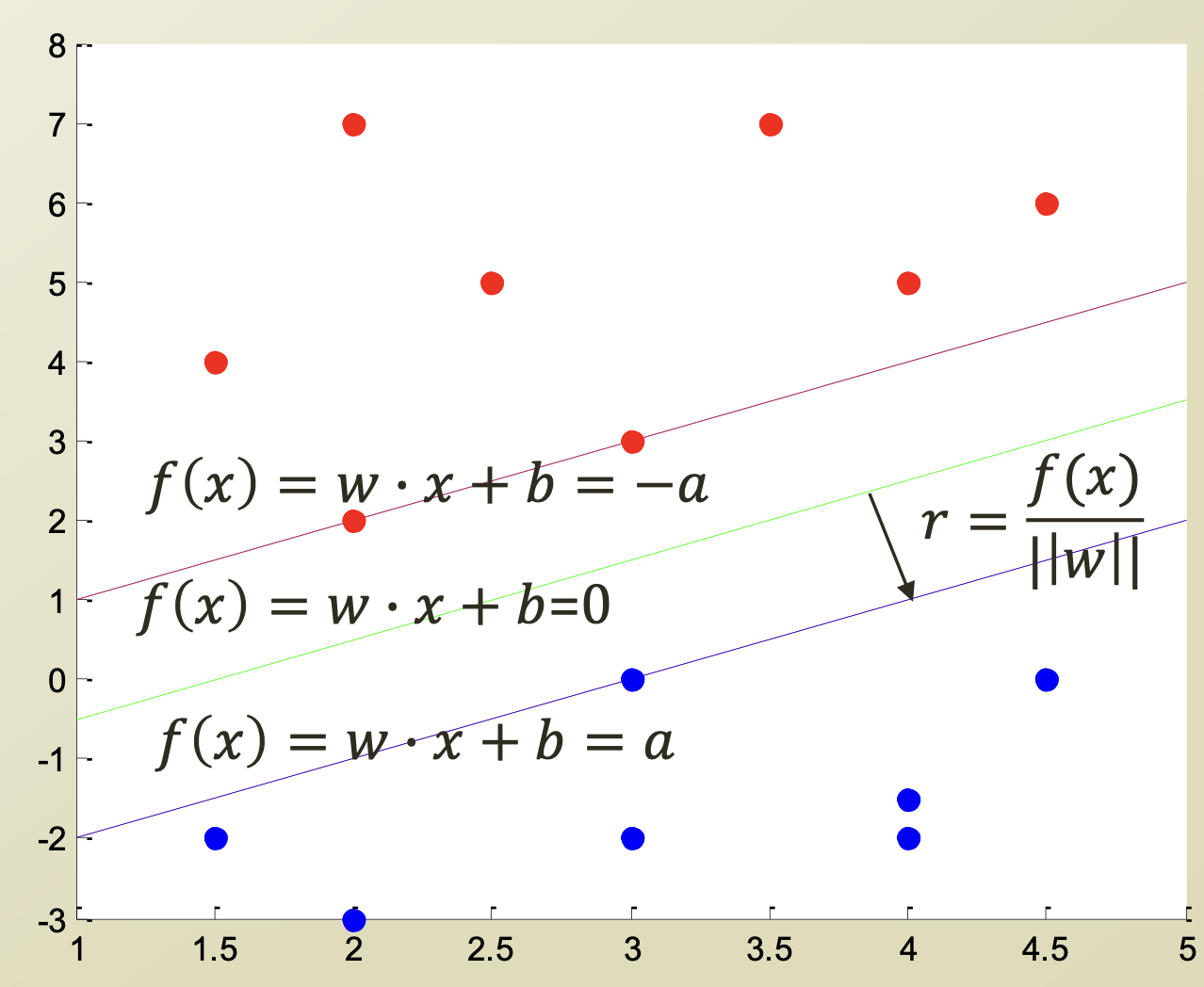
Decision boundary가 위와 같을 때, margin distance는 $2r$ 이므로,
margin distance $= {2a \over ||w||}$ 이다.

margin distance이 최대가 되도록 하기 위해서 해결해야 하는 optimization problem은 다음과 같다.
$max_{w,b}2r = {2a \over ||w||}$
결국 해결해야할 optimization problem은 $min_{w,b}||w||$ 로 나타낼 수 있다.

4. Error cases in SVM

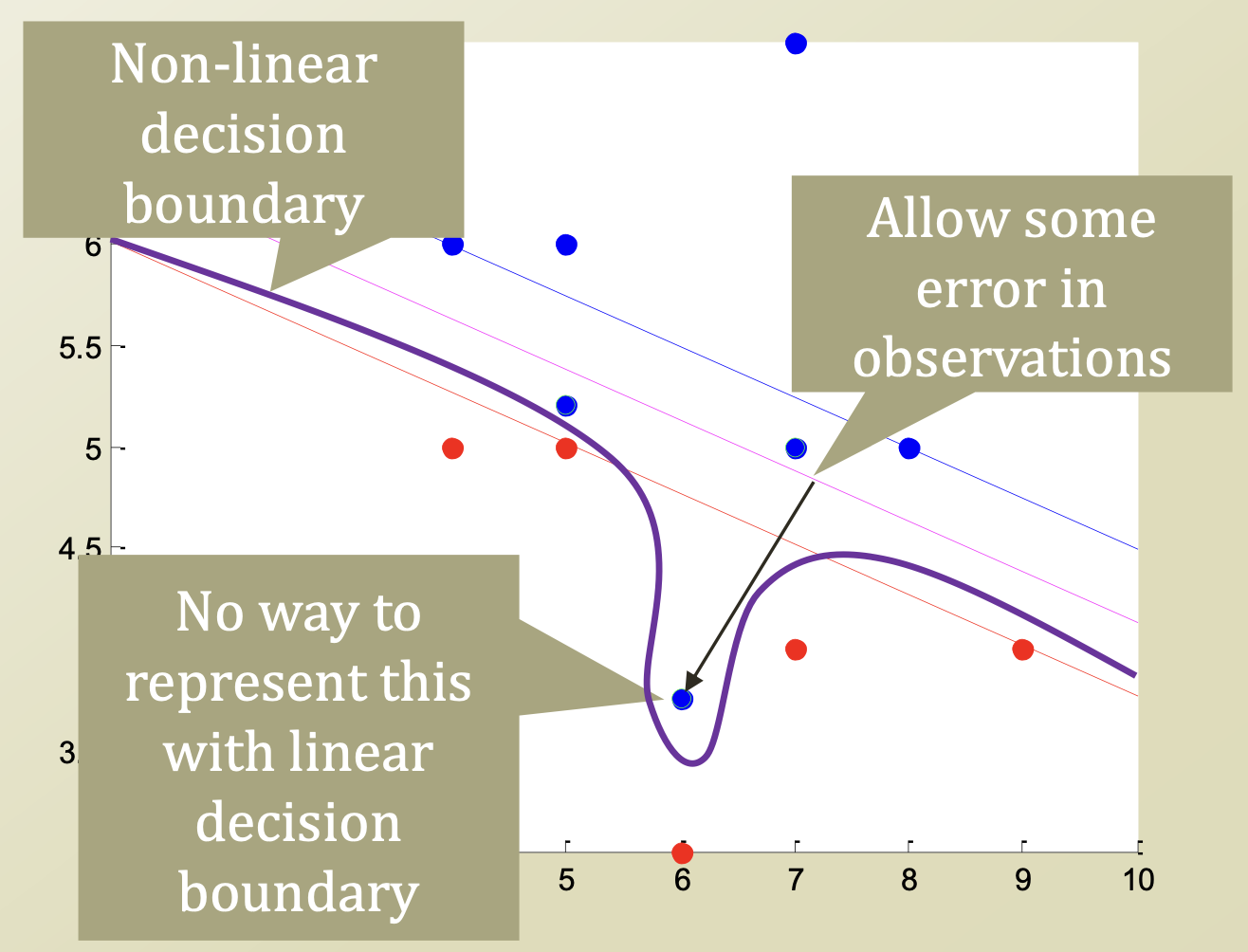
=> 이와 같이 error case가 존재할 때, 이를 어떻게 해결해야할까?

• Option 1
  Make Decision Boundary more complex
  => non linear한 Decision boundary로 다시 설정함.
• Option 2
  Admit there will be an "error"
  => error data로 인정하고, 그에 대해 penalty를 부과함.
• Error Handling in SVM
• Option 1 : Error case의 갯수를 세어, 그 수만큼 페널티를 부과함.
  $min_{w,b}||w||+ C \times #_{error}$
• Option 2 : Error case가 Decision boundary로부터 얼마나 떨어져 있는지에 따라, 페널티를 다르게 부과함.
  $min_{w,b}||w||+ C \sum_j\xi_j$
  ($\xi$ = slack variable : Loss function)
  
  
  0-1 Loss의 경우 Option 1과 같이 Decision Boundary를 넘어가면 penalty가 1로 고정되는 것이고, Hinge Loss의 경우 Decision Boundary로부터 거리가 멀어질수록 penalty가 커진다.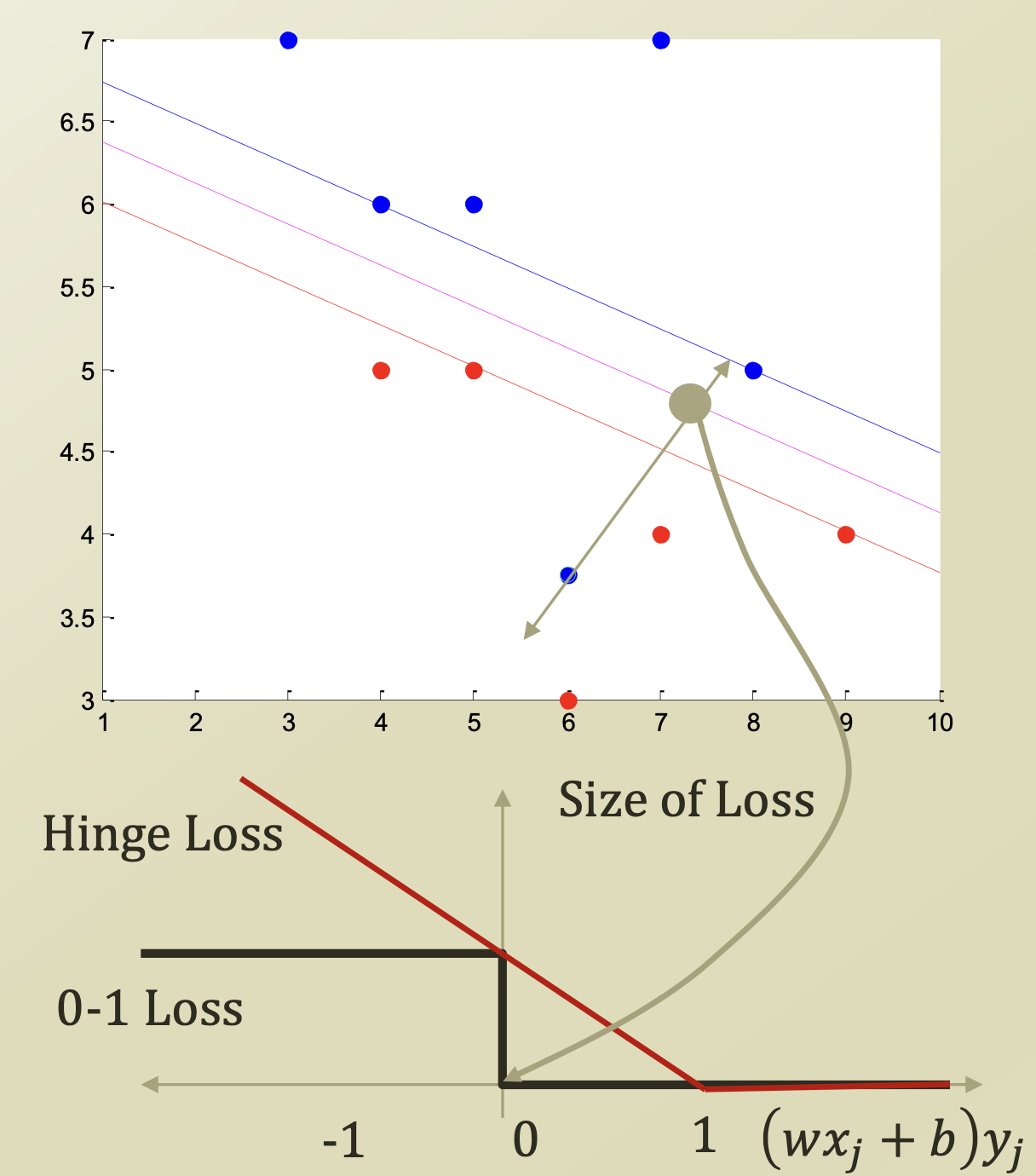
• Loss function
  $\xi_j = (1 - (wx_j + b)y_j)_+$ => hinge loss
  $\xi_j = - log(P(Y_j|X_j, w, b)) = log(1 + e^{(wx_j + b)y_j})$ => log loss
  
  
  우리가 해결해야할 optimization problem은 다음과 같다.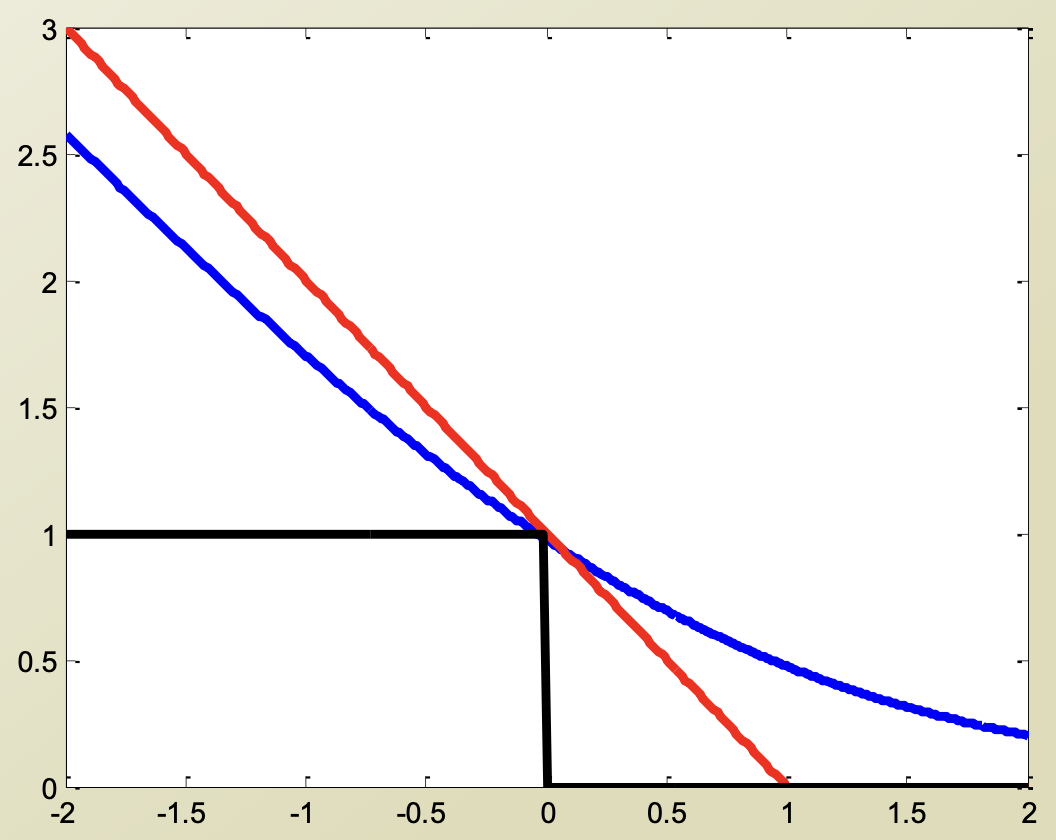
  $min_{w,b}||w||$
  $s.t.$ $(wx_j + b)y_j\geq1, \forall j$
• 5. Dual Problem of SVM

이 problem을 Lagrange Dual problem으로 바꾸면 다음과 같다.
$max_{\alpha \geq0} min_{w,b}{1\over2}w\cdot w - \sum_j\alpha_j[(wx_j + b)y_j -1]$
$s.t.\alpha_j\geq0, for$ $\forall j$
(Lagrange Dual Problem에 관해서는 다음 post에서 설명하겠습니다.)

여기서 strong duality를 만족하기 위해서 KKT Condition을 만족해야하므로,

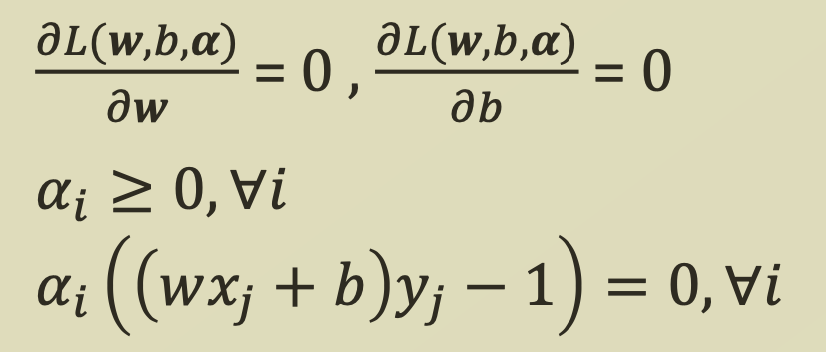
위 식들을 함께 정리해보면

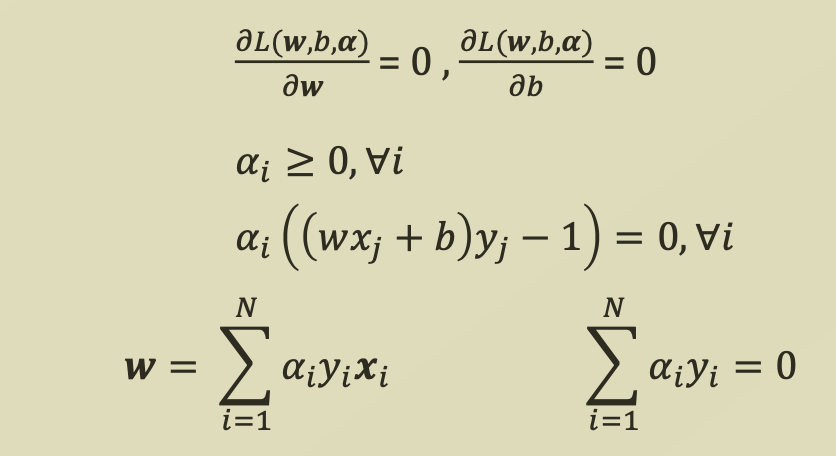
다음과 같은 조건들을 도출할 수 있다.

이 조건들을 통해 Lagrange problem을 정리해 보면, 다음과 같이 정리된다.

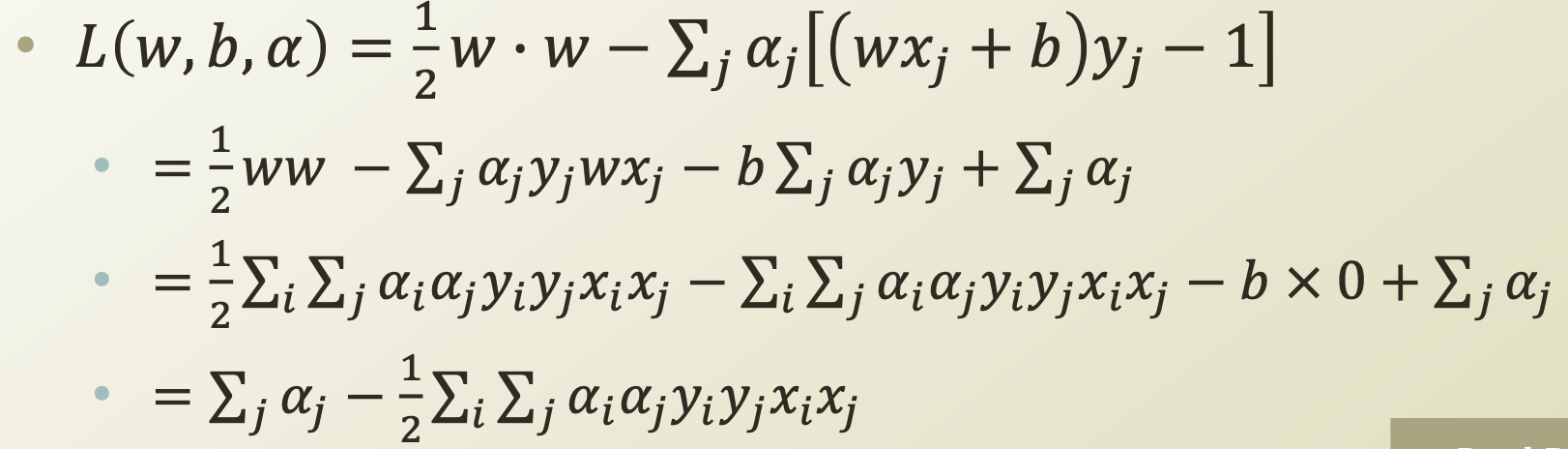
=> 이 식은 $w$에 관한 식이 $\alpha$에 관한 식으로 변경되었다는 점에서 의의가 있다.

6. Kernel Trick

=> non-linear한 Decision boudary를 더 쉽게 설정하기 위해 하는 trick이다.

• Mapping Function
  => Linearly separable하지 않은 data들에 대해서, 더 높은 차원의 data로 mapping시킴으로써, linearly separable하도록 만드는 함수
  
  
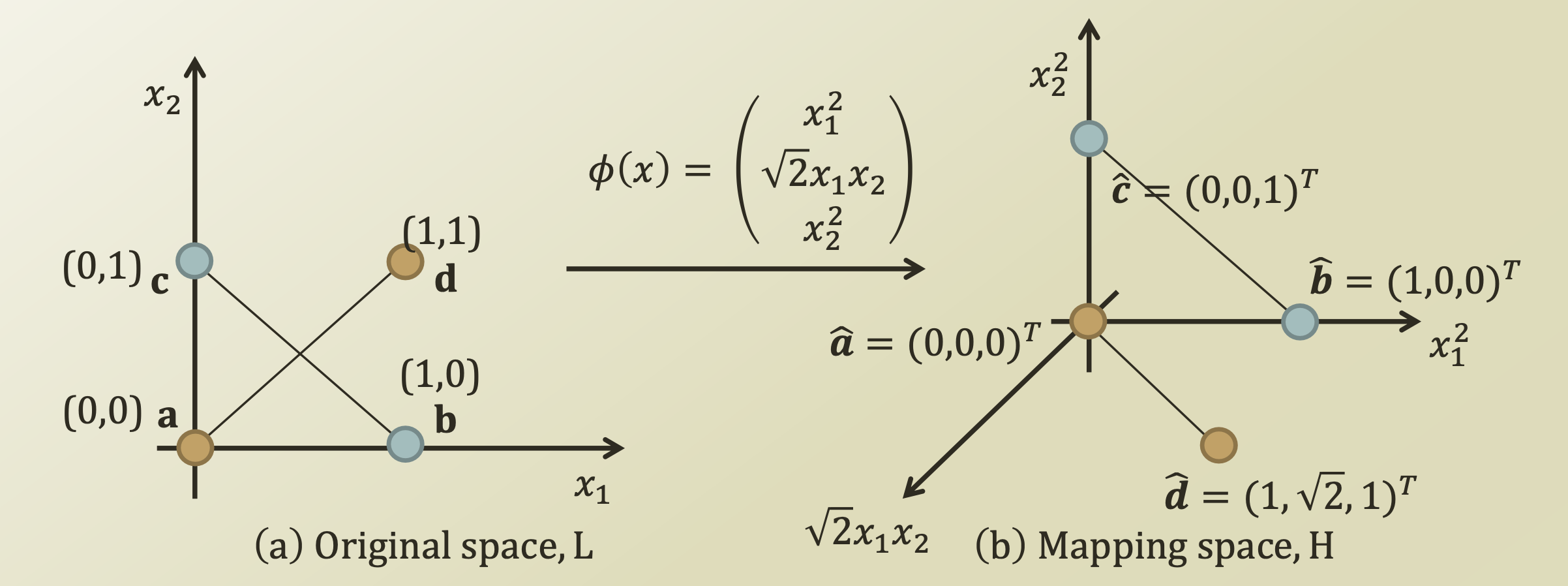
• Kernel Function
  => 두 data를 mapping function을 통해 다른 차원으로 보낸 후 내적한 것
  $K(x_i, x_j) = \phi(x_i)\cdot\phi(x_j)$위와 같은 Polynomial Kernel Function외에 다양한 kernel function이 있다.
  
  
• 예를 들어, $\phi(x) = (x_1^2, \sqrt2 x_1x_2, x_2^2)$ 라고 할 때, Kernel function으로 나타내 보자.
  $\textbf{x} = <x_1, x_2>$, $\textbf{z} = <z_1, z_2>$
  $K(<x_1, x_2>,<z_1,z_2>) =$
  $<x_1^2, \sqrt2 x_1x_2, x_2^2> \cdot <x_1^2, \sqrt2 x_1x_2, x_2^2>$
  $= (x_1z_1+x_2z_2)^2 = (\textbf{x} \cdot \textbf{z})^2$
  위의 식 처럼 복잡해보이는 두 mapping function을 내적함에 따라, 간단하게 나타낼 수 있다.

7. Dual SVM with Kernel Trick

이제 SVM을 Dual problem으로 나타낸 식에 Kernel Trick을 적용해보자.
Data의 차원을 높이기 위해 mapping 시키면 다음과 같이 w와 b의 식을 정리할 수 있다.

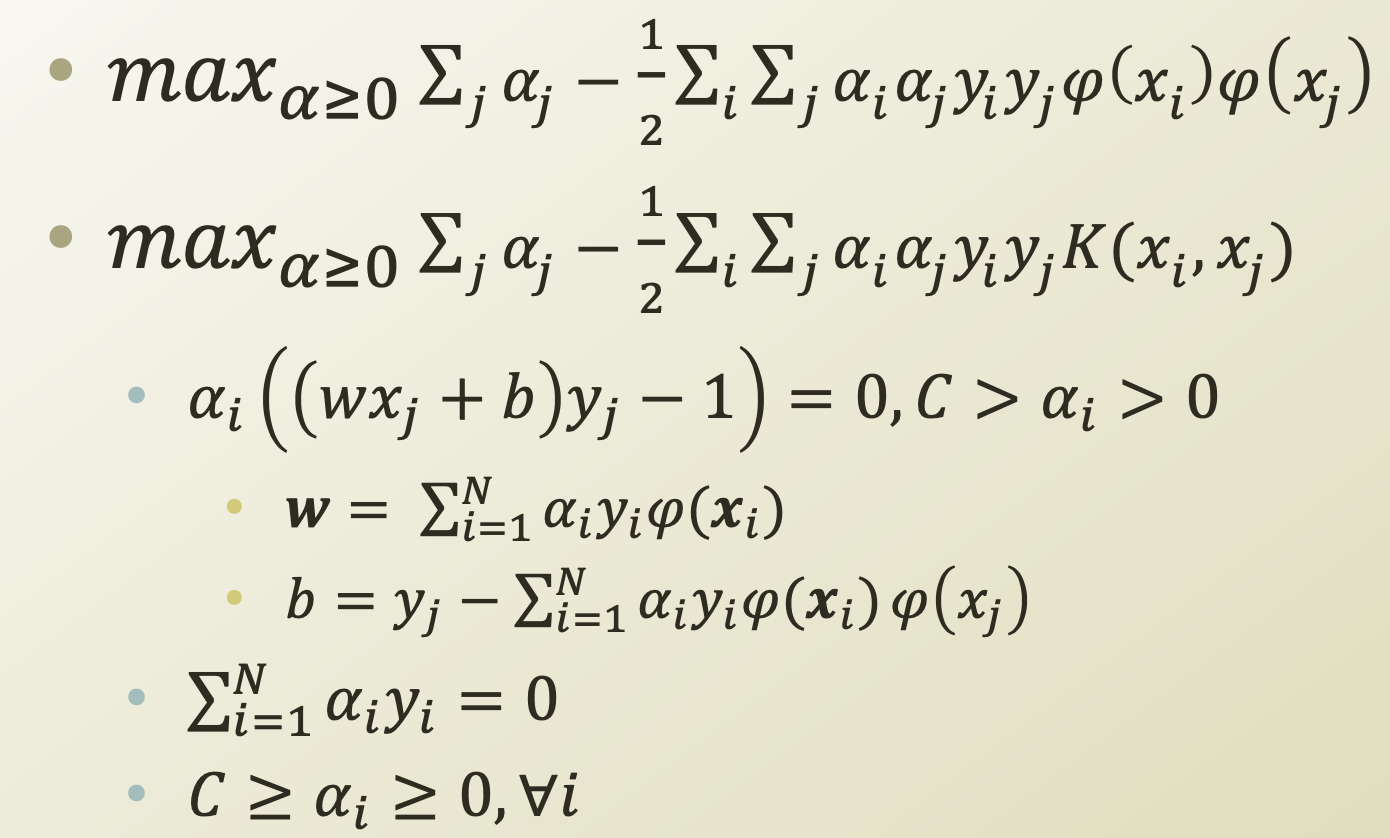
여기서 우리의 목적은 새로운 data가 들어왔을 때, Decision boundary식인 wx + b에 넣어 음수인지 양수인지 판단해 data를 분류하는 것이므로, 우리가 판단 해야할 식은 $sign(w\cdot x + b)$이다.

이 식에 커널 트릭을 적용하면 다음과 같다.

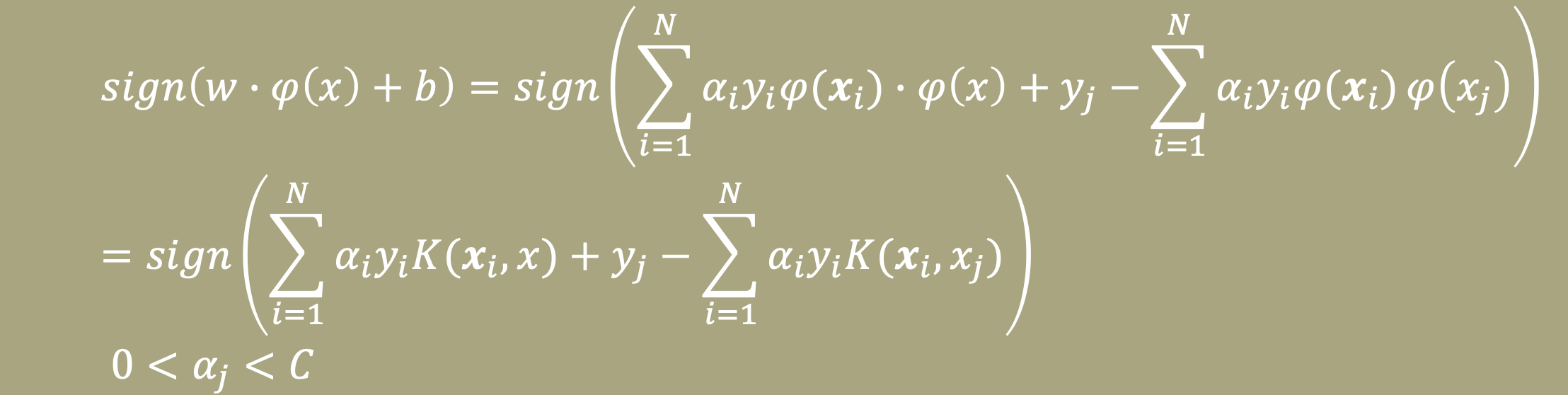
Reference

[1]https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/
[2]https://hleecaster.com/ml-svm-concept/
[3]https://sanghyu.tistory.com/14